- Research Article
- Open access
- Published:
An Order on Subsets of Cone Metric Spaces and Fixed Points of Set-Valued Contractions
Fixed Point Theory and Applications volume 2009, Article number: 723203 (2009)
Abstract
In this paper at first we introduce a new order on the subsets of cone metric spaces then, using this definition, we simplify the proof of fixed point theorems for contractive set-valued maps, omit the assumption of normality, and obtain some generalization of results.
1. Introduction and Preliminary
Cone metric spaces were introduced by Huang and Zhang [1]. They replaced the set of real numbers by an ordered Banach space and obtained some fixed point theorems for mapping satisfying different contractions [1]. The study of fixed point theorems in such spaces followed by some other mathematicians, see [2–8]. Recently Wardowski [9] was introduced the concept of set-valued contractions in cone metric spaces and established some end point and fixed point theorems for such contractions. In this paper at first we will introduce a new order on the subsets of cone metric spaces then, using this definition, we simplify the proof of fixed point theorems for contractive set-valued maps, omit the assumption of normality, and obtain some generalization of results.
Let  be a real Banach space. A nonempty convex closed subset
be a real Banach space. A nonempty convex closed subset  is called a cone in
is called a cone in  if it satisfies.
if it satisfies.
(i) is closed, nonempty, and
is closed, nonempty, and  ,
,
(ii)
 and
and  imply that
imply that 
(iii) and
and  imply that
imply that 
The space  can be partially ordered by the cone
can be partially ordered by the cone  ; that is,
; that is,  if and only if
if and only if  . Also we write
. Also we write  if
if 
 , where
, where  denotes the interior of
denotes the interior of  .
.
A cone  is called normal if there exists a constant
is called normal if there exists a constant  such that
such that  implies
implies  .
.
In the following we always suppose that  is a real Banach space,
is a real Banach space,  is a cone in
is a cone in  and
and  is the partial ordering with respect to
is the partial ordering with respect to  .
.
Definition 1.1 (see [1]).
Let  be a nonempty set. Assume that the mapping
be a nonempty set. Assume that the mapping  satisfies
satisfies
(i) for all
for all  and
and  iff
iff 
(ii) for all
for all 
(iii) for all
for all  .
.
Then  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space.
is called a cone metric space.
In the following we have some necessary definitions.
(1)Let  be a cone metric space. A set
be a cone metric space. A set  is called closed if for any sequence
is called closed if for any sequence  convergent to
convergent to  , we have
, we have 
(2)A set  is called sequentially compact if for any sequence
is called sequentially compact if for any sequence  , there exists a subsequence
, there exists a subsequence  of
of  is convergent to an element of
is convergent to an element of 
(3)Denote  a collection of all nonempty subsets of
a collection of all nonempty subsets of  ,
,  a collection of all nonempty closed subsets of
a collection of all nonempty closed subsets of  and
and  a collection of all nonempty sequentially compact subsets of
a collection of all nonempty sequentially compact subsets of 
(4)An element  is said to be an endpoint of a set-valued map
is said to be an endpoint of a set-valued map  if
if  We denote a set of all endpoints of
We denote a set of all endpoints of  by
by 
(5)An element  is said to be a fixed point of a set-valued map
is said to be a fixed point of a set-valued map  if
if  Denote
Denote 
(6)A map  is called lower semi-continuous, if for any sequence
is called lower semi-continuous, if for any sequence  in
in  and
and  such that
such that  as
as  , we have
, we have 
(7)A map  is called have lower semi-continuous property, and denoted by lsc property if for any sequence
is called have lower semi-continuous property, and denoted by lsc property if for any sequence  in
in  and
and  such that
such that  as
as  , then there exists
, then there exists  that
that  for all
for all 
(8) called minihedral cone if
called minihedral cone if  exists for all
exists for all  , and strongly minihedral if every subset of
, and strongly minihedral if every subset of  which is bounded from above has a supremum [10]. Let
which is bounded from above has a supremum [10]. Let  a cone metric space, cone
a cone metric space, cone  is strongly minihedral and hence, every subset of
is strongly minihedral and hence, every subset of  has infimum, so for
has infimum, so for  , we define
, we define 
Example 1.2.
Let  with
with  . The cone
. The cone  is normal, minihedral and strongly minihedral with
is normal, minihedral and strongly minihedral with  .
.
Example 1.3.
Let  be a compact set,
be a compact set,  and
and  . The cone
. The cone  is normal and minihedral but is not strongly minihedral and
is normal and minihedral but is not strongly minihedral and  .
.
Example 1.4.
Let  be a finite measure space,
be a finite measure space,  countably generated,
countably generated,  ,
,  and
and  . The cone
. The cone  is normal, minihedral and strongly minihedral with
is normal, minihedral and strongly minihedral with  .
.
For more details about above examples, see [11].
Example 1.5.
Let  with norm
with norm  and
and  that is not normal cone by [12] and not minihedral by [10].
that is not normal cone by [12] and not minihedral by [10].
Example 1.6.
Let  and
and  . This
. This  is strongly minihedral but not minihedral by [10].
is strongly minihedral but not minihedral by [10].
Throughout, we will suppose that  is strongly minihedral cone in
is strongly minihedral cone in  with nonempty interior and
with nonempty interior and  be a partial ordering with respect to
be a partial ordering with respect to 
2. Main Results
Let  be a cone metric space and
be a cone metric space and  . For
. For  Let
Let

At first we prove the closedness of  without the assumption of normality.
without the assumption of normality.
Lemma 2.1.
Let  be a complete cone metric space and
be a complete cone metric space and  . If the function
. If the function  for
for  is lower semi-continuous, then
is lower semi-continuous, then  is closed.
is closed.
Proof.
Let  and
and  We show that
We show that  Since
Since

so  which implies
which implies  for some
for some  . Let
. Let  with
with  then, there exists
then, there exists  such that for
such that for  ,
,  Now, for
Now, for  we have,
we have,

So  is a Cauchy sequence in complete metric space, hence there exist
is a Cauchy sequence in complete metric space, hence there exist  such that
such that  . Since
. Since  is closed, thus
is closed, thus  Now by uniqueness of limit we conclude that
Now by uniqueness of limit we conclude that 
Definition 2.2.
Let  and
and  are subsets of
are subsets of  , we write
, we write  if and only if there exist
if and only if there exist  such that for all
such that for all  ,
,  Also for
Also for  , we write
, we write  if and only if
if and only if  and similarly
and similarly  if and only if
if and only if 
Note that  , for every scaler
, for every scaler  and
and  subsets of
subsets of  .
.
The following lemma is easily proved.
Lemma 2.3.
Let  ,
,  ,
,  and
and  .
.
(1)If  and
and  then
then 
(2)
(3)If  then
then 
(4)If  then
then 
(5)
(6)If  then
then 
The order " " is not antisymmetric, thus this order is not partially order.
" is not antisymmetric, thus this order is not partially order.
Example 2.4.
Let  and
and  . Put
. Put  and
and  so
so  but
but 
Theorem 2.5.
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map and the function
, a set-valued map and the function  defined by
defined by  ,
,  with lsc property. If there exist real numbers
with lsc property. If there exist real numbers  and
and  with
with  such that for all
such that for all  there exists
there exists  :
:

then 
Proof.
Let  , then there exists
, then there exists  such that
such that

Let  , there exist
, there exist  such that
such that  and
and  Continuing this process, we can iteratively choose a sequence
Continuing this process, we can iteratively choose a sequence  in
in  such that
such that  ,
,  and
and  So, for
So, for  we have,
we have,

Therefore, for every  ,
,  Let
Let  and
and  be given. Choose
be given. Choose  such that
such that  where
where  Also, choose a
Also, choose a  such that
such that  for all
for all  Then
Then  for all
for all  Thus
Thus  for all
for all  Namely,
Namely,  is Cauchy sequence in complete cone metric space, therefore
is Cauchy sequence in complete cone metric space, therefore  for some
for some  Now we show that
Now we show that 
Let  hence there exists
hence there exists  such that
such that  for all
for all  Now
Now  as
as  so for all
so for all  there exists
there exists  such that
such that  for all
for all 
According to lsc property of  , for all
, for all  there exists
there exists  such that for all
such that for all 

So  for all
for all  Namely,
Namely,  thus
thus  for some
for some  and by the closedness of
and by the closedness of  we have
we have 
We notice that  implies that for all
implies that for all  there exists
there exists  such that
such that  for all
for all  but the inverse is not true.
but the inverse is not true.
Example 2.6.
Let  with norm
with norm  and
and  that is not normal cone by [12]. Consider
that is not normal cone by [12]. Consider  and
and  so
so  and
and  , (see [10]) Define cone metric
, (see [10]) Define cone metric  with
with  , for
, for 
 . Since
. Since  namely,
namely,  but
but  . Indeed
. Indeed  in
in  but
but  in
in  Even for
Even for 
 and
and  in particular
in particular  but
but  .
.
Example 2.7.
Let  with norm
with norm  and
and  that is not normal cone. Define cone metric
that is not normal cone. Define cone metric  with
with  , for
, for 
 and set-valued mapping
and set-valued mapping  by
by  . In this space every Cauchy sequence converges to zero. The function
. In this space every Cauchy sequence converges to zero. The function  have lsc property. Also we have
have lsc property. Also we have  and
and  . Now for
. Now for 


 and for all
and for all  take
take  . Therefore, it satisfies in all of the hypothesis of Theorem 2.5. So
. Therefore, it satisfies in all of the hypothesis of Theorem 2.5. So  has a fixed point
has a fixed point  For sample take
For sample take 
 and
and 
Theorem 2.8.
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map, and a function
, a set-valued map, and a function  defined by
defined by  ,
,  with lsc property. The following conditions hold:
with lsc property. The following conditions hold:
(i)if there exist real numbers  and
and  with
with  such that for all
such that for all  there exists
there exists  :
:

then 
(ii)if there exist real numbers  and
and  with
with  such that for all
such that for all  and
and  :
:

then 
Proof.
-
(i)
It is obvious that
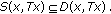 It is enough to show that
It is enough to show that  for all
for all  However
However 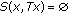 for some
for some 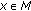 , it implies
, it implies 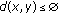 for some
for some 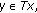 and this is a contradiction.
and this is a contradiction. -
(ii)
By (i), there exists
 such that
such that 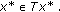 Then for
Then for 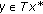 and
and  we have
we have  . Therefore,
. Therefore, 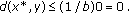 This implies that
This implies that 
Corollary 2.9.
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map, and the function
, a set-valued map, and the function  defined by
defined by  , for
, for  with lsc property. If there exist real numbers
with lsc property. If there exist real numbers  and
and  with
with  such that for all
such that for all  there exists
there exists  with
with

then 
To have Theorems??3.1 and ??3.2 in [9], as the corollaries of our theorems we need the following lemma and remarks.
Lemma 2.10.
Let  be a cone metric space,
be a cone metric space,  a normal cone with constant one and
a normal cone with constant one and  , a set-valued map, then
, a set-valued map, then

Proof.
Put  and
and  we show that
we show that 
Let  then
then  and so
and so  which implies
which implies 
For the inverse, let for all  . Then
. Then  for all
for all 
Since  , for every
, for every  that
that  there exists
there exists  such that
such that  so
so  for all
for all  Thus
Thus 
Remark 2.11.
By Proposition ?1.7.59, page 117 in [11], if  is an ordered Banach space with positive cone
is an ordered Banach space with positive cone  , then
, then  is a normal cone if and only if there exists an equivalent norm
is a normal cone if and only if there exists an equivalent norm  on
on  which is monotone. So by renorming the
which is monotone. So by renorming the  we can suppose
we can suppose  is a normal cone with constant one.
is a normal cone with constant one.
Remark 2.12.
Let  be a cone metric space,
be a cone metric space,  a normal cone with constant one,
a normal cone with constant one,  , a set-valued map, the function
, a set-valued map, the function  defined by
defined by  ,
,  with lsc property, and
with lsc property, and  with
with  . Then
. Then  is lower semi-continuous.
is lower semi-continuous.
Now the Theorems ?3.1 and ?3.2 in [9] is stated as the following corollaries without the assumption of normality, and by Lemma ?2.10 and Remarks ?2.11, ?2.12 we have the same theorems.
Corollary 2.13 (see [9, Theorem ?3.1]).
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map and the function
, a set-valued map and the function  defined by
defined by  ,
,  with lsc property. If there exist real numbers
with lsc property. If there exist real numbers  ,
,  such that for all
such that for all  there exists
there exists  one has
one has  and
and  then
then 
Corollary 2.14 (see [9, Theorem ?3.2]).
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map and the function
, a set-valued map and the function  defined by
defined by  ,
,  with lsc property. The following hold:
with lsc property. The following hold:
(i)if there exist real numbers  ,
,  such that for all
such that for all  there exists
there exists  one has
one has  and
and  then
then 
(ii)if there exist real numbers  ,
,  such that for all
such that for all  and every
and every  one has
one has  and
and  then
then 
Definition 2.15.
For  ,
,  where
where  is a set-valued map we define
is a set-valued map we define

Note that  for
for 
The following theorem is a reform of Theorem 2.5.
Theorem 2.16.
Let  be a complete cone metric space,
be a complete cone metric space,  , a set-valued map, and the function
, a set-valued map, and the function  defined by
defined by  ,
,  with lsc property. If there exists
with lsc property. If there exists  such that
such that

for all  Then
Then 
Proof.
For every  , then there exist
, then there exist  and
and  such that
such that  , for all
, for all  . Let
. Let  , there exist
, there exist  and
and  such that
such that  since
since  . Thus
. Thus  The remaining is same as the proof of Theorem 2.5.
The remaining is same as the proof of Theorem 2.5.
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Abbas M, Rhoades BE: Fixed and periodic point results in cone metric spaces. Applied Mathematics Letters 2009,22(4):511–515. 10.1016/j.aml.2008.07.001
Arshad M, Azam A, Vetro P: Some common fixed point results in cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-11.
Ilic D, Rakocevic V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Ilic D, Rakocevic V: Quasi-contraction on a cone metric space. Applied Mathematics Letters 2009,22(5):728–731. 10.1016/j.aml.2008.08.011
Jankovic S, Kadelburg Z, Radenovic S, Rhoades BE: Assad-Kirk-type fixed point theorems for a pair of nonself mappings on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-16.
Jungck G, Radenovic S, Radojevic S, Rakocevic V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-13.
Raja P, Vaezpour SM: Some extensions of Banach's contraction principle in complete cone metric spaces. Fixed Point Theory and Applications 2008, 2008:-11.
Wardowski D: Endpoints and fixed points of set-valued contractions in cone metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(1–2):512–516. 10.1016/j.na.2008.10.089
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Denkowski Z, Migórski S, Papageorgiou NS: An Introduction to Nonlinear Analysis: Applications. Kluwer Academic Publishers, Boston, Mass, USA; 2003:xii+823.
Rezapour Sh, Hamlbarani R: Some notes on the paper "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Asadi, M., Soleimani, H. & Vaezpour, S.M. An Order on Subsets of Cone Metric Spaces and Fixed Points of Set-Valued Contractions. Fixed Point Theory Appl 2009, 723203 (2009). https://doi.org/10.1155/2009/723203
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/723203
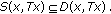 It is enough to show that
It is enough to show that  for all
for all  However
However 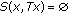 for some
for some 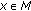 , it implies
, it implies 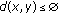 for some
for some 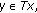 and this is a contradiction.
and this is a contradiction. such that
such that 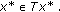 Then for
Then for 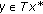 and
and  we have
we have  . Therefore,
. Therefore, 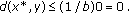 This implies that
This implies that 