- Research Article
- Open access
- Published:
Common Fixed Point Theorems in Menger Probabilistic Quasimetric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 546273 (2009)
Abstract
We consider complete Menger probabilistic quasimetric space and prove common fixed point theorems for weakly compatible maps in this space.
1. Introduction and Preliminaries
K. Menger introduced the notion of a probabilistic metric space in 1942 and since then the theory of probabilistic metric spaces has developed in many directions [1]. The idea of  Menger was to use distribution functions instead of nonnegative real numbers as values of the metric. The notion of a probabilistic metric space corresponds to the situations when we do not know exactly the distance between two points, we know only probabilities of possible values of this distance. Such a probabilistic generalization of metric spaces appears to be well adapted for the investigation of physiological thresholds and physical quantities particularly in connections with both string and
Menger was to use distribution functions instead of nonnegative real numbers as values of the metric. The notion of a probabilistic metric space corresponds to the situations when we do not know exactly the distance between two points, we know only probabilities of possible values of this distance. Such a probabilistic generalization of metric spaces appears to be well adapted for the investigation of physiological thresholds and physical quantities particularly in connections with both string and  theory; see [2–5]. It is also of fundamental importance in probabilistic functional analysis, nonlinear analysis and applications [6–10].
theory; see [2–5]. It is also of fundamental importance in probabilistic functional analysis, nonlinear analysis and applications [6–10].
In the sequel, we will adopt usual terminology, notation, and conventions of the theory of Menger probabilistic metric spaces, as in [7, 8, 10]. Throughout this paper, the space of all probability distribution functions (in short, dfs) is denoted by  is left-continuous and nondecreasing on
is left-continuous and nondecreasing on  ,
,  and
and  and the subset
and the subset  is the set
is the set  . Here
. Here  denotes the left limit of the function
denotes the left limit of the function  at the point
at the point  ,
,  . The space
. The space  is partially ordered by the usual pointwise ordering of functions, that is,
is partially ordered by the usual pointwise ordering of functions, that is,  if and only if
if and only if  for all
for all  in
in  . The maximal element for
. The maximal element for  in this order is the df given by
in this order is the df given by

Definition 1.1 (see [1]).
A mapping  is
is  if
if  is satisfying the following conditions:
is satisfying the following conditions:
(a) is commutative and associative;
is commutative and associative;
(b) for all
for all  ;
;
(d) whenever
whenever  and
and  , and
, and  .
.
The following are the four basic  :
:

Each 
 can be extended [11] (by associativity) in a unique way to an
can be extended [11] (by associativity) in a unique way to an  -ary operation taking for
-ary operation taking for  the values
the values  and
and

for  and
and  , for all
, for all  .
.
We also mention the following families of 
Definition 1.2.
It is said that the  -norm
-norm  is of Hadžić-type (
is of Hadžić-type ( for short) and
for short) and  if the family
if the family  of its iterates defined, for each
of its iterates defined, for each  in
in  , by
, by

is equicontinuous at  , that is,
, that is,

There is a nice characterization of continuous 
 of the class
of the class  [12].
[12].
(i)If there exists a strictly increasing sequence  in
in  such that
such that  and
and  , then
, then  is of Hadžić-type.
is of Hadžić-type.
(ii)If  is continuous and
is continuous and  , then there exists a sequence
, then there exists a sequence  as in (i).The
as in (i).The 
 is an trivial example of a
is an trivial example of a  of
of  but there are
but there are 
 of Hadžić-type with
of Hadžić-type with  (see, e.g., [13]).
(see, e.g., [13]).
Definition 1.3 (see [13]).
If  is a
is a  and
and  , then
, then  is defined recurrently by 1, if
is defined recurrently by 1, if  and
and  for all
for all  . If
. If  is a sequence of numbers from
is a sequence of numbers from  then
then  is defined as
is defined as  (this limit always exists) and
(this limit always exists) and  as
as  . In fixed point theory in probablistic metric spaces there are of particular interest the
. In fixed point theory in probablistic metric spaces there are of particular interest the  -norms
-norms  and sequences
and sequences  such that
such that  and
and  . Some examples of
. Some examples of  with the above property are given in the following proposition.
with the above property are given in the following proposition.
Proposition 1.4 (see [13]).
-
(i)
For
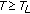 the following implication holds:
the following implication holds:

-
(ii)
If
 , then for every sequence
, then for every sequence 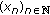 in I such that
in I such that 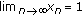 , one has
, one has 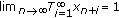 .
.
Note [14, Remark 13] that if  is a
is a  for which there exists
for which there exists  such that
such that  and
and  , then
, then  Important class of
Important class of  is given in the following example.
is given in the following example.
Example 1.5.
-
(i)
The Dombi family of
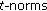
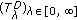 is defined by
is defined by

 The Aczél-Alsina family of
The Aczél-Alsina family of 
 is defined by
is defined by

 Sugeno-Weber family of
Sugeno-Weber family of 
 is defined by
is defined by

In [13] the following results are obtained.
(a)If  is the Dombi family of
is the Dombi family of  and
and  is a sequence of elements from
is a sequence of elements from  such that
such that  then we have the following equivalence:
then we have the following equivalence:

(b)Equivalence (1.10) holds also for the family  that is,
that is,

(c)If  is the Sugeno-Weber family of
is the Sugeno-Weber family of  and
and  is a sequence of elements from
is a sequence of elements from  such that
such that  then we have the following equivalence:
then we have the following equivalence:

Proposition 1.6.
Let  be a sequence of numbers from
be a sequence of numbers from  such that
such that  and
and  -norm
-norm  is of
is of  . Then
. Then

Definition 1.7.
A Menger Probabilistic Quasimetric space (briefly, Menger PQM space) is a triple  , where
, where  is a nonempty set,
is a nonempty set,  is a continuous
is a continuous  , and
, and  is a mapping from
is a mapping from  into
into  such that, if
such that, if  denotes the value of
denotes the value of  at the pair
at the pair  , then the following conditions hold, for all
, then the following conditions hold, for all  in
in  ,
,
(PQM1) for all
for all  if and only if
if and only if  ;
;
(PQM2) for all
for all  and
and  .
.
Definition 1.8.
Let  be a Menger PQM space.
be a Menger PQM space.
(1)A sequence  in
in  is said to be convergent to
is said to be convergent to  in
in  if, for every
if, for every  and
and  , there exists positive integer
, there exists positive integer  such that
such that  whenever
whenever  .
.
(2)A sequence  in
in  is called Cauchy sequence [15] if, for every
is called Cauchy sequence [15] if, for every  and
and  , there exists positive integer
, there exists positive integer  such that
such that  whenever
whenever  (
( ).
).
(3)A Menger PQM space  is said to be complete if and only if every Cauchy sequence in
is said to be complete if and only if every Cauchy sequence in  is convergent to a point in
is convergent to a point in  .
.
In 1998, Jungck and Rhoades [16] introduced the following concept of weak compatibility.
Definition 1.9.
Let  and
and  be mappings from a Menger PQM space
be mappings from a Menger PQM space  into itself. Then the mappings are said to be weak compatible if they commute at their coincidence point, that is,
into itself. Then the mappings are said to be weak compatible if they commute at their coincidence point, that is,  implies that
implies that  .
.
2. The Main Result
Throughout this section, a binary operation  is a continuous
is a continuous  -norm and satisfies the condition
-norm and satisfies the condition

where  . It is easy to see that this condition implies
. It is easy to see that this condition implies  .
.
Lemma 2.1.
Let  be a Menger PQM space. If the sequence
be a Menger PQM space. If the sequence  in X is such that for every
in X is such that for every 

for very  , where
, where  is a monotone increasing functions.Then the sequence
is a monotone increasing functions.Then the sequence  is a Cauchy sequence.
is a Cauchy sequence.
Proof.
For every  and
and  , we have
, we have

for each  and
and  . Hence sequence
. Hence sequence  is Cauchy sequence.
is Cauchy sequence.
Theorem 2.2.
Let  be a complete Menger PQM space and let
be a complete Menger PQM space and let  be maps that satisfy the following conditions:
be maps that satisfy the following conditions:
(a) ;
;
(b)the pairs  and
and  are weak compatible,
are weak compatible,  is closed subset of
is closed subset of  ;
;
(c) for all
for all  and every
and every  , where
, where  is a monotone increasing function.
is a monotone increasing function.
If

then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Let  . By (a), we can find
. By (a), we can find  such that
such that  and
and  . By induction, we can define a sequence
. By induction, we can define a sequence  such that
such that  and
and  . By induction again,
. By induction again,

Similarly, we have

Hence, it follows that

for 
Now by Lemma 2.1,  is a Cauchy sequence. Since the space
is a Cauchy sequence. Since the space  is complete, there exists a point
is complete, there exists a point  such that
such that

It follows that, there exists  such that
such that  . We prove that
. We prove that  . From (c), we get
. From (c), we get

as  , we have
, we have

which implies that,  . Moreover,
. Moreover,

as  , we have
, we have

which implies that  Since, the pairs
Since, the pairs  and
and  are weak compatible, we have
are weak compatible, we have  hence it follows that
hence it follows that  Similarly, we get
Similarly, we get  Now, we prove that
Now, we prove that  Since, from (c) we have
Since, from (c) we have

as  , we have
, we have

It follows that  . Therefore,
. Therefore,  . That is
. That is  is a common fixed point of
is a common fixed point of  and
and  .
.
If  and
and  are two fixed points common to
are two fixed points common to  and
and  , then
, then

as  , which implies that
, which implies that  and so the uniqueness of the common fixed point.
and so the uniqueness of the common fixed point.
Corollary 2.3.
Let  be a complete Menger PQM space and let
be a complete Menger PQM space and let  be maps that satisfy the following conditions:
be maps that satisfy the following conditions:
(a) ;
;
(b)the pair  is weak compatible,
is weak compatible,  is closed subset of
is closed subset of  ;
;
(c) for all
for all  and
and  where
where  is monotone increasing function.
is monotone increasing function.
If

then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
It is enough, set  in Theorem 2.2.
in Theorem 2.2.
Corollary 2.4.
Let  be a complete Menger PQM space and let
be a complete Menger PQM space and let  be maps that satisfy the following conditions:
be maps that satisfy the following conditions:
(a)
(b)the pair  is weak compatible,
is weak compatible,  is closed subset of
is closed subset of  ;
;
(c) for all
for all  and
and  , where
, where  is monotone increasing function;
is monotone increasing function;
-
(d)
 (2.17)
(2.17)
If

then  have a unique common fixed point.
have a unique common fixed point.
Proof.
By Corollary 2.3, if set  then
then  have a unique common fixed point in
have a unique common fixed point in  . That is, there exists
. That is, there exists  , such that
, such that  . We prove that
. We prove that  , for
, for  From (c), we have
From (c), we have

By (d), we get

Hence,  . Thus ,
. Thus ,  .
.
Similarly, we have  .
.
Corollary 2.5.
Let  be a complete PQM space and let
be a complete PQM space and let  satisfy conditions (a), (b), and (c) of Theorem 2.2. If
satisfy conditions (a), (b), and (c) of Theorem 2.2. If  is a
is a  of
of  then there exists a unique common fixed point for the mapping
then there exists a unique common fixed point for the mapping  and
and  .
.
Proof.
By Proposition 1.6 all the conditions of the Theorem 2.2 are satisfied.
Corollary 2.6.
Let  for some
for some  be a complete PQM space and let
be a complete PQM space and let  satisfy conditions (a), (b), and (c) of Theorem 2.2. If
satisfy conditions (a), (b), and (c) of Theorem 2.2. If  then there exists a unique common fixed point for the mapping
then there exists a unique common fixed point for the mapping  and
and  .
.
Proof.
From equivalence (1.10) we have

Corollary 2.7.
Let  for some
for some  be a complete PQM space and let
be a complete PQM space and let  satisfy conditions (a), (b), and (c) of Theorem 2.2. If
satisfy conditions (a), (b), and (c) of Theorem 2.2. If  then there exists a unique common fixed point for the mapping
then there exists a unique common fixed point for the mapping  and
and  .
.
Proof.
From equivalence (1.11) we have

Corollary 2.8.
Let  for some
for some  be a complete PQM space and let
be a complete PQM space and let  satisfy conditions (a), (b), and (c) of Theorem 2.2. If
satisfy conditions (a), (b), and (c) of Theorem 2.2. If  then there exists a unique common fixed point for the mapping
then there exists a unique common fixed point for the mapping  and
and  .
.
Proof.
From equivalence (1.12) we have

References
Schweizer B, Sklar A: Probabilistic Metric Spaces, North-Holland Series in Probability and Applied Mathematics. North-Holland, New York, NY, USA; 1983:xvi+275.
El Naschie MS: On the uncertainty of Cantorian geometry and the two-slit experiment. Chaos, Solitons & Fractals 1998,9(3):517–529. 10.1016/S0960-0779(97)00150-1
El Naschie MS: A review of infinity theory and the mass spectrum of high energy particle physics. Chaos, Solitons & Fractals 2004,19(1):209–236. 10.1016/S0960-0779(03)00278-9
El Naschie MS: On a fuzzy Kähler-like manifold which is consistent with the two slit experiment. International Journal of Nonlinear Sciences and Numerical Simulation 2005,6(2):95–98. 10.1515/IJNSNS.2005.6.2.95
El Naschie MS: The idealized quantum two-slit gedanken experiment revisited-Criticism and reinterpretation. Chaos, Solitons & Fractals 2006,27(4):843–849. 10.1016/j.chaos.2005.06.002
Chang SS, Lee BS, Cho YJ, Chen YQ, Kang SM, Jung JS: Generalized contraction mapping principle and differential equations in probabilistic metric spaces. Proceedings of the American Mathematical Society 1996,124(8):2367–2376. 10.1090/S0002-9939-96-03289-3
Chang S-S, Cho YJ, Kang SM: Nonlinear Operator Theory in Probabilistic Metric Spaces. Nova Science Publishers, Huntington, NY, USA; 2001:x+338.
Khamsi MA, Kreinovich VY: Fixed point theorems for dissipative mappings in complete probabilistic metric spaces. Mathematica Japonica 1996,44(3):513–520.
Razani A: A contraction theorem in fuzzy metric spaces. Fixed Point Theory and Applications 2005,2005(3):257–265. 10.1155/FPTA.2005.257
Schweizer B, Sherwood H, Tardiff RM: Contractions on probabilistic metric spaces: examples and counterexamples. Stochastica 1988,12(1):5–17.
Klement EP, Mesiar R, Pap E: Triangular Norms, Trends in Logic—Studia Logica Library. Volume 8. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xx+385.
Radu V: Lectures on Probabilistic Analysis, Surveys, Lecture Notes and Monographs.Series on Probability, Statistics and Applied Mathematics. Volume 2. Universitatea din Timisoara, Timisoara, Romania; 1994.
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Mathematics and Its Applications. Volume 536. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+273.
Hadžić O, Pap E: New classes of probabilistic contractions and applications to random operators. In Fixed Point Theory and Applications (Chinju/Masan, 2001). Volume 4. Nova Science Publishers, Hauppauge, NY, USA; 2003:97–119.
Reilly IL, Subrahmanyam PV, Vamanamurthy MK: Cauchy sequences in quasipseudometric spaces. Monatshefte für Mathematik 1982,93(2):127–140. 10.1007/BF01301400
Jungck G, Rhoades BE: Fixed points for set valued functions without continuity. Indian Journal of Pure and Applied Mathematics 1998,29(3):227–238.
Acknowledgment
The second author is supported by MNTRRS 144012.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sedghi, S., Žikić-Došenović, T. & Shobe, N. Common Fixed Point Theorems in Menger Probabilistic Quasimetric Spaces. Fixed Point Theory Appl 2009, 546273 (2009). https://doi.org/10.1155/2009/546273
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/546273
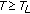 the following implication holds:
the following implication holds: , then for every sequence
, then for every sequence 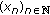 in I such that
in I such that 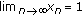 , one has
, one has 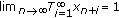 .
.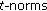
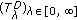 is defined by
is defined by