- Research Article
- Open access
- Published:
Strong Convergence Theorem by Monotone Hybrid Algorithm for Equilibrium Problems, Hemirelatively Nonexpansive Mappings, and Maximal Monotone Operators
Fixed Point Theory and Applications volume 2008, Article number: 617248 (2008)
Abstract
We introduce a new hybrid iterative algorithm for finding a common element of the set of fixed points of hemirelatively nonexpansive mappings and the set of solutions of an equilibrium problem and for finding a common element of the set of zero points of maximal monotone operators and the set of solutions of an equilibrium problem in a Banach space. Using this theorem, we obtain three new results for finding a solution of an equilibrium problem, a fixed point of a hemirelatively nonexpnasive mapping, and a zero point of maximal monotone operators in a Banach space.
1. Introduction
Let  be a Banach space, let
be a Banach space, let  be a closed convex subset of
be a closed convex subset of  , and let
, and let  be a bifunction from
be a bifunction from  to
to  , where
, where  is the set of real numbers. The equilibrium problem is to find
is the set of real numbers. The equilibrium problem is to find

The set of such solutions  is denoted by
is denoted by  .
.
In 2006, Martinez-Yanes and Xu [1] obtained strong convergence theorems for finding a fixed point of a nonexpansive mapping by a new hybrid method in a Hilbert space. In particular, Takahashi and Zembayashi [2] established a strong convergence theorem for finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a nonexpansive mapping in a uniformly convex and uniformly smooth Banach space. Very recently, Su et al. [3] proved the following theorem by a monotone hybrid method.
Theorem 1.1 (see Su et al. [3]).
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a closed hemirelatively nonexpansive mapping such that
be a closed hemirelatively nonexpansive mapping such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  by the following:
by the following:

where  is the duality mapping on
is the duality mapping on  . Then,
. Then,  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
In this paper, motivated by Su et al. [3], we prove a strong convergence theorem for finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a hemirelatively nonexpansive mapping and for finding a common element of the set of zero points of maximal monotone operators and the set of solutions of an equilibrium problem in a Banach space by using the monotone hybrid method. Using this theorem, we obtain three new strong convergence results for finding a solution of an equilibrium problem, a fixed point of a hemirelatively nonexpnasive mapping, and a zero point of maximal monotone operators in a Banach space.
2. Preliminaries
Let  be a real Banach space with dual
be a real Banach space with dual  . We denote by
. We denote by  the normalized duality mapping from
the normalized duality mapping from  to
to  defined by
defined by

where  denotes the generalized duality pairing. It is well known that if
denotes the generalized duality pairing. It is well known that if  is uniformly convex, then
is uniformly convex, then  is uniformly continuous on bounded subsets of
is uniformly continuous on bounded subsets of  . In this case,
. In this case,  is single valued and also one to one.
is single valued and also one to one.
Let  be a smooth, strictly convex, and reflexive Banach space and let
be a smooth, strictly convex, and reflexive Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Throughout this paper, we denote by
. Throughout this paper, we denote by  the function defined by
the function defined by

Following Alber [4], the generalized projection  from
from  onto
onto  is defined by
is defined by

The generalized projection  from
from  onto
onto  is well defined and single valued, and it satisfies
is well defined and single valued, and it satisfies

If  is a Hilbert space, then
is a Hilbert space, then  and
and  is the metric projection of
is the metric projection of  onto
onto  .
.
If  is a reflexive strict convex and smooth Banach space, then for
is a reflexive strict convex and smooth Banach space, then for  if and only if
if and only if  . It is sufficient to show that if
. It is sufficient to show that if  , then
, then  . From (2.4), we have
. From (2.4), we have  . This implies
. This implies  . From the definition of
. From the definition of  , we have
, we have  , that is,
, that is,  .
.
Let  be a closed convex subset of
be a closed convex subset of  and let
and let  be a mapping from
be a mapping from  into itself. We denote by
into itself. We denote by  the set of fixed points of
the set of fixed points of  .
.  is called hemirelatively nonexpansive if
is called hemirelatively nonexpansive if  for all
for all  and
and  .
.
A point  in
in  is said to be an asymptotic fixed point of
is said to be an asymptotic fixed point of  [5] if
[5] if  contains a sequence
contains a sequence  which converges weakly to
which converges weakly to  such that the strong
such that the strong  . The set of asymptotic fixed points of
. The set of asymptotic fixed points of  will be denoted by
will be denoted by  . A hemirelatively nonexpansive mapping
. A hemirelatively nonexpansive mapping  from
from  into itself is called relatively nonexpansive [1, 5, 6] if
into itself is called relatively nonexpansive [1, 5, 6] if  .
.
We need the following lemmas for the proof of our main results.
Lemma 2.1 (see Alber [4]).
Let  be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space
be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space  . Then,
. Then,

Lemma 2.2 (see Alber [4]).
Let  be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space, let
be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space, let  , and let
, and let  . Then,
. Then,

Lemma 2.3 (see Kamimura and Takahashi [7]).
Let  be a smooth and uniformly convex Banach space and let
be a smooth and uniformly convex Banach space and let  and
and  be sequences in
be sequences in  such that either
such that either  or
or  is bounded. If
is bounded. If  . Then
. Then  .
.
Lemma 2.4 (see Xu [8]).
Let  be a uniformly convex Banach space and let
be a uniformly convex Banach space and let  . Then, there exists a strictly increasing, continuous, and convex function
. Then, there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

where  .
.
Lemma 2.5 (see Kamimura and Takahashi [7]).
Let  be a smooth and uniformly convex Banach space and let
be a smooth and uniformly convex Banach space and let  . Then, there exists a strictly increasing, continuous, and convex function
. Then, there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

For solving the equilibrium problem, let us assume that a bifunction  satisfies the following conditions:
satisfies the following conditions:
-
(A1)
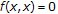 for all
for all 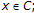
-
(A2)
 is monotone, that is,
is monotone, that is, 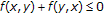 for all
for all 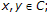
-
(A3) for all
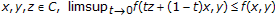 ;
; -
(A4) for all
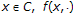 is convex.
is convex.
Lemma 2.6 (see Blum and Oettli [9]).
Let  be a closed convex subset of a smooth, strictly convex, and reflexive Banach space
be a closed convex subset of a smooth, strictly convex, and reflexive Banach space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), let
satisfying (A1)–(A4), let  , and let
, and let  . Then, there exists
. Then, there exists  such that
such that

Lemma 2.7 (see Takahashi and Zembayashi [10]).
Let  be a closed convex subset of a uniformly smooth, strictly convex, and reflexive Banach space
be a closed convex subset of a uniformly smooth, strictly convex, and reflexive Banach space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  , for
, for  . Define a mapping
. Define a mapping  as follows:
as follows:

Then, the following holds:
-
(1)
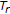 is single valued;
is single valued; -
(2)
 is a firmly nonexpansive-type mapping [11], that is, for all
is a firmly nonexpansive-type mapping [11], that is, for all 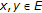 ,
,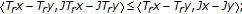 (211)
(211) -
(3)
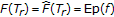 ;
; -
(4)
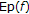 is closed and convex.
is closed and convex.
Lemma 2.8 (see Takahashi and Zembayashi [10]).
Let  be a closed convex subset of a smooth, strictly convex, and reflexive Banach space
be a closed convex subset of a smooth, strictly convex, and reflexive Banach space  and let
and let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4). Then, for
satisfying (A1)–(A4). Then, for  and
and  , and
, and  ,
,

Lemma 2.9 (see Su et al. [3]).
Let  be a strictly convex and smooth real Banach space, let
be a strictly convex and smooth real Banach space, let  be a closed convex subset of
be a closed convex subset of  , and let
, and let  be a hemirelatively nonexpansive mapping from
be a hemirelatively nonexpansive mapping from  into itself. Then,
into itself. Then,  is closed and convex.
is closed and convex.
Recall that an operator  in a Banach space is called closed, if
in a Banach space is called closed, if  , then
, then  .
.
3. Strong Convergence Theorem
Theorem 3.1.
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a closed hemirelatively nonexpansive mapping such that
be a closed hemirelatively nonexpansive mapping such that  . Define a sequence
. Define a sequence  in
in  by the following:
by the following:

for every  , where
, where  is the duality mapping on
is the duality mapping on  are sequences in
are sequences in  such that
such that  and
and  for some
for some  . Then,
. Then,  converges strongly to
converges strongly to  , where
, where  is the generalized projection of
is the generalized projection of  onto
onto  .
.
Proof.
First, we can easily show that  and
and  are closed and convex for each
are closed and convex for each  .
.
Next, we show that  for all
for all  . Let
. Let  . Putting
. Putting  for all
for all  , from Lemma 2.8, we have
, from Lemma 2.8, we have  relatively nonexpansive. Since
relatively nonexpansive. Since  are relatively nonexpansive and
are relatively nonexpansive and  is hemirelatively nonexpansive, we have
is hemirelatively nonexpansive, we have

Hence, we have

Next, we show that  for all
for all  . We prove this by induction. For
. We prove this by induction. For  , we have
, we have

Suppose that  , by Lemma 2.2, we have
, by Lemma 2.2, we have

As  , by the induction assumptions, the last inequality holds, in particular, for all
, by the induction assumptions, the last inequality holds, in particular, for all  . This, together with the definition of
. This, together with the definition of  , implies that
, implies that  . So,
. So,  is well defined.
is well defined.
Since  and
and  for all
for all  , we have
, we have

Therefore,  is nondecreasing. In addition, from the definition of
is nondecreasing. In addition, from the definition of  and Lemma 2.2,
and Lemma 2.2,  . Therefore, for each
. Therefore, for each  , we have
, we have

Therefore,  and
and  are bounded. This, together with (3.6), implies that the limit of
are bounded. This, together with (3.6), implies that the limit of  exists. From Lemma 2.1, we have, for any positive integer
exists. From Lemma 2.1, we have, for any positive integer  ,
,

Therefore,

From (3.9), we can prove that  is a Cauchy sequence. Therefore, there exists a point
is a Cauchy sequence. Therefore, there exists a point  such that
such that  converges strongly to
converges strongly to  .
.
Since  , we have
, we have

Therefore, we have

From Lemma 2.3, we have

So, we have

Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

Let  Since
Since  is a uniformly smooth Banach space, we know that
is a uniformly smooth Banach space, we know that  is a uniformly convex Banach space. Therefore, from Lemma 2.4, there exists a continuous, strictly increasing, and convex function
is a uniformly convex Banach space. Therefore, from Lemma 2.4, there exists a continuous, strictly increasing, and convex function  with
with  , such that
, such that

for  , and
, and  . So, we have that for
. So, we have that for  ,
,

Therefore, we have

Since

we have

From  , we have
, we have

Therefore, from the property of  , we have
, we have

Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

Since  is a closed operator and
is a closed operator and  , then
, then  is a fixed point of
is a fixed point of  .
.
On the other hand,

So, we have from (3.19) that

From Lemma 2.3, we have that

From  and
and  , we have
, we have  .
.
From (3.25), we have

From  , we have
, we have

By  , we have
, we have

From (A2), we have that

From (3.27) and (A4), we have

For  with
with  and
and  , let
, let  . We have
. We have  . So, from (A1), we have
. So, from (A1), we have

Dividing by  , we have
, we have

Letting  , from (A3), we have
, from (A3), we have

Therefore,  . Finally, we prove that
. Finally, we prove that  . From Lemma 2.1, we have
. From Lemma 2.1, we have

Since  and
and  , for all
, for all  , we get from Lemma 2.1 that
, we get from Lemma 2.1 that

By the definition of  , it follows that
, it follows that  and
and  , whence
, whence  . Therefore, it follows from the uniqueness of
. Therefore, it follows from the uniqueness of  that
that  . This completes the proof.
. This completes the proof.
Corollary 3.2.
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4). Define a sequence
satisfying (A1)–(A4). Define a sequence  in
in  by the following:
by the following:

for every  , where
, where  is the duality mapping on
is the duality mapping on  and
and  for some
for some  . Then,
. Then,  converges strongly to
converges strongly to  .
.
Proof.
Putting  in Theorem 3.1, we obtain Corollary 3.2.
in Theorem 3.1, we obtain Corollary 3.2.
Corollary 3.3.
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a closed hemirelatively nonexpansive mapping. Define a sequence
be a closed hemirelatively nonexpansive mapping. Define a sequence  in
in  by the following:
by the following:

for every  , where
, where  is the duality mapping on
is the duality mapping on  are sequences in
are sequences in  such that
such that  . Then,
. Then,  converges strongly to
converges strongly to  .
.
Proof.
Putting  for all
for all  and
and  for all
for all  in Theorem 3.1, we obtain Corollary 3.3.
in Theorem 3.1, we obtain Corollary 3.3.
Corollary 3.4.
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a closed relatively nonexpansive mapping such that
be a closed relatively nonexpansive mapping such that  . Define a sequence
. Define a sequence  in
in  by the following:
by the following:

for every  , where
, where  is the duality mapping on
is the duality mapping on  are sequences in
are sequences in  such that
such that  and
and  for some
for some  . Then,
. Then,  converges strongly to
converges strongly to  .
.
Proof.
Since every relatively nonexpansive mapping is a hemirelatively one, Corollary 3.4 is implied by Theorem 3.1.
Remark 3.5 (see Rockafellar [12]).
Let  be a reflexive, strictly convex, and smooth Banach space and let
be a reflexive, strictly convex, and smooth Banach space and let  be a monotone operator from
be a monotone operator from  to
to  . Then,
. Then,  is maximal if and only if
is maximal if and only if  for all
for all  .
.
Let  be a reflexive, strictly convex, and smooth Banach space and let
be a reflexive, strictly convex, and smooth Banach space and let  be a maximal monotone operator from
be a maximal monotone operator from  to
to  . Using Remark 3.5 and strict convexity of
. Using Remark 3.5 and strict convexity of  , we obtain that for every
, we obtain that for every  and
and  , there exists a unique
, there exists a unique  such that
such that  If
If  , then we can define a single-valued mapping
, then we can define a single-valued mapping  by
by  , and such a
, and such a  is called the resolvent of
is called the resolvent of  . We know that
. We know that  for all
for all  and
and  is relatively nonexpansive mapping (see [2] for more details). Using Theorem 3.1, we can consider the problem of strong convergence concerning maximal monotone operators in a Banach space.
is relatively nonexpansive mapping (see [2] for more details). Using Theorem 3.1, we can consider the problem of strong convergence concerning maximal monotone operators in a Banach space.
Theorem 3.6.
Let  be a uniformly convex and uniformly smooth real Banach space, let
be a uniformly convex and uniformly smooth real Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a resolvent of
be a resolvent of  and a closed mapping such that
and a closed mapping such that  , where
, where  . Define a sequence
. Define a sequence  in
in  by the following:
by the following:

for every  , where
, where  is the duality mapping on
is the duality mapping on  ,
,  is a sequences in
is a sequences in  such that
such that  and
and  for some
for some  , Then,
, Then,  converges strongly to
converges strongly to  .
.
Proof.
Since  is a closed relatively nonexpansive mapping and
is a closed relatively nonexpansive mapping and  , from Corollary 3.4, we obtain Theorem 3.6.
, from Corollary 3.4, we obtain Theorem 3.6.
References
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2400-2411. 10.1016/j.na.2005.08.018
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-11.
Su Y, Wang D, Shang M: Strong convergence of monotone hybrid algorithm for hemi-relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Edited by: Kartsatos AG. Marcel Dekker, New York, NY, USA; 1996:15-50.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. Journal of Applied Analysis 2001, 7(2):151-174. 10.1515/JAA.2001.151
Matsushita S-Y, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005, 134(2):257-266. 10.1016/j.jat.2005.02.007
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002, 13(3):938-945. 10.1137/S105262340139611X
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991, 16(12):1127-1138. 10.1016/0362-546X(91)90200-K
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123-145.
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):45-57. 10.1016/j.na.2007.11.031
Kohsaka F, Takahashi W: Existence and approximation of fixed points of firmly nonexpansive type mappings in Banach spaces. to appear in SIAM Journal on Optimization
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75-88. 10.1090/S0002-9947-1970-0282272-5
Acknowledgment
This work is supported by Tianjin Natural Science Foundation in China Grant no. 06YFJMJC12500.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, Y., Tian, M. Strong Convergence Theorem by Monotone Hybrid Algorithm for Equilibrium Problems, Hemirelatively Nonexpansive Mappings, and Maximal Monotone Operators. Fixed Point Theory Appl 2008, 617248 (2008). https://doi.org/10.1155/2008/617248
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/617248
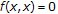 for all
for all 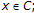
 is monotone, that is,
is monotone, that is, 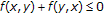 for all
for all 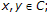
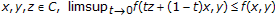 ;
;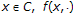 is convex.
is convex.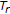 is single valued;
is single valued; is a firmly nonexpansive-type mapping [
is a firmly nonexpansive-type mapping [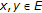 ,
,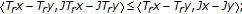
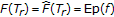 ;
;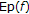 is closed and convex.
is closed and convex.